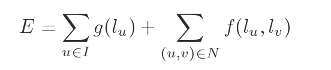
Abstract
Many problems of image processing lead to the minimization of an energy, which is a function of one or several given images, with respect to a binary or multi-label image. When this energy is made of unary data terms and of pairwise regularization terms, and when the pairwise regularization term is a metric, the multi-label energy can be minimized quite rapidly, using the so-called α-expansion algorithm. α-expansion consists in decomposing the multi-label optimization into a series of binary sub-problems called move. Depending on the chosen decomposition, a different condition on the regularization term applies. The metric condition for α-expansion move is rather restrictive. In many cases, the statistical model of the problem leads to an energy which is not a metric. Based on the enlightening article 1, we derive another condition for α-jump move. Finally, we propose an alternated scheme which can be used even if the energy fulfills neither the α-expansion nor β-jump condition. The proposed scheme applies to a much larger class of regularization functions, compared to α-expansion. This opens many possibilities of improvements on diverse image processing problems. We illustrate the advantages of the proposed optimization scheme on the image noise reduction problem.
Bibtex
@inproceedings{jpt-icip15,
author = {Paget, M. and Tarel, J.-P. and Caraffa, L.},
title = {Extending $\alpha$-expansion to a larger set of regularization functions},
booktitle = {Proceedings of IEEE International Conference on Image Processing (ICIP'15)},
date = {September 27-30},
address = {Qu\'ebec City, Canada},
pages = {1051--1055},
year = {2015},
note = {http://perso.lcpc.fr/tarel.jean-philippe/publis/icip15.html}
}
Footnotes:
Endre Boros and Peter L. Hammer. 2002. Pseudo-boolean optimization. Discrete Appl. Math. 123, 1-3 (November 2002), 155-225. DOI=http://dx.doi.org/10.1016/S0166-218X(01)00341-9